En este apartado vas a encontrar de manera muy detallada los contenidos que necesitas para resolver ciertos problemas de matrices.
En este apartado vas a encontrar de manera muy detallada los contenidos que necesitas para resolver ciertos problemas de matrices.
1.1 Definición de matriz
Las matrices son una de las herramientas más usadas del Álgebra Lineal y están asociadas a un conjunto de datos numéricos ordenados. Encontramos las matrices en muchas ciencias: Sociología, Economía, Demografía, Física, Biología, etc.
La idea intuitiva de matriz es muy sencilla, pudiéndose, definir como una tabla de números ordenados, números que pueden provenir de experimentos, encuestas, análisis económicos, etc.
Por tanto:
Se llama matriz de orden m x n a un conjunto de números reales dispuestos en m filas y en n columnas de la forma:
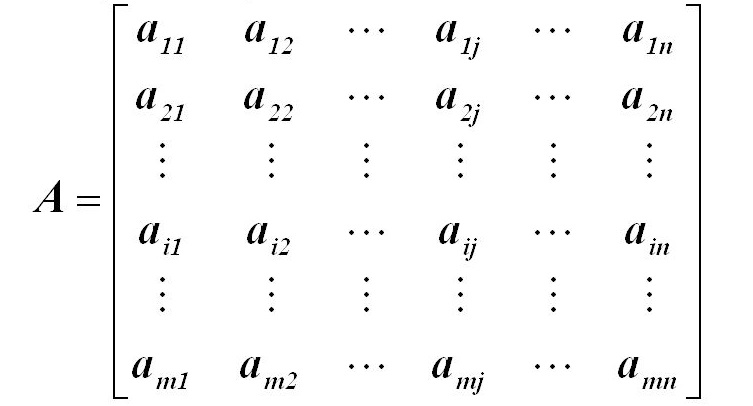
Las matrices se representan por letras mayúsculas A, B, C, … Los elementos de la matriz (los números) se representan en general por aij, donde los subíndices (i,j) nos dan la posición que ocupa el término: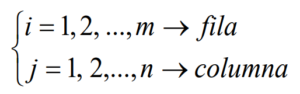
Así el término a13 es el elemento que está en la primera fila y en la tercera columna.
1.2. Dimensión de una matriz
El número de filas (m) y el número de columnas (n) nos da la dimensión de la matriz m x n.
Ejemplo:
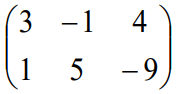es una matriz de dimensión 2 x 3.1.3. Igualdad de matrices
Dos matrices son iguales si tienen la misma dimensión y si los términos que ocupan la misma posición son iguales:
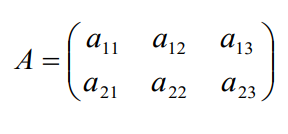
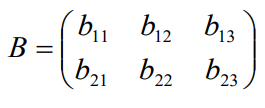
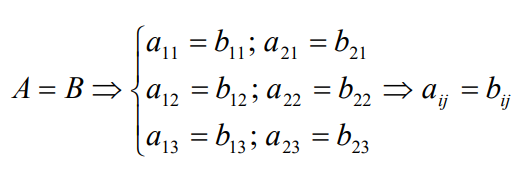
Ejemplo:
Si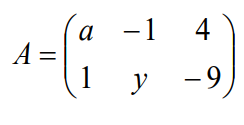 
y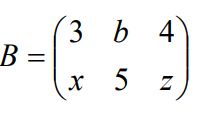 
para que A = B debe cumplirse que:
a = 3 , b = -1 , y = 5 y z =-9.